GIMNAZIJA
AKTUELNO
Forum
SAJTOVI
ZANIMLJIVO
Gradivo za takmičenje u Gimnaziji "Veljko Petrović"
Računarstvo i Informatika
Grafovi
Obilazak grafa pretraživanjem u dubinu - DFS - (depth first search)
Ovo je klasičan rekurzivni algoritam (dinamičkim programiranjem). Postupak je sledeći: Pođemo od nekog čvora u grafu i posetimo njegovog prvog suseda, zatim prvog suseda prvog suseda, i sve tako u dubinu dok ima prvih suseda koje još nismo posetili. Tada se vratimo u prethodni čvor i proverimo da li ima neki od njegovih suseda kog nismo posetili. Ako ima, tada se spuštamo u tu granu u dubinu dokle god je to moguće i sve tako dok ne posetimo sve čvorove.
Posetu nekom čvoru beležimo u globalni niz Idx.
Implementacija DFS-a
Ako nam je bitan redosled posete čvorovima, tada uvodimo i globalnu promenljivu Lbl, a ako nam redosled nije bitan, možemu upisivati i jedinicu na odg. mesto u Idx.
Niz Idx, i promenljivu Lbl treba isprazniti pre poziva DFS-a. I G je ovaj put globalna.
Var Idx : array [1..MaxN] of Integer;
Lbl : Integer;
G : TGraf;
Procedure DFS(v : TCvor);
var w : TCvor;
Begin
Lbl := Lbl + 1;
Idx[v] := Lbl;
w := SledeciSused(G, v, 0);
while w <> 0 do
Begin
if Idx[w] = 0 then DFS(w);
w := SledeciSused(G, v, w);
End;
End;
Nakon izvršenja ove procedure, znamo da smo posetili čvor v, ako je Idx[v] <> 0.
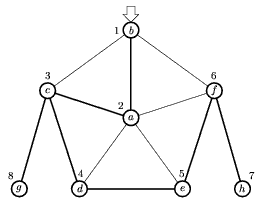
Kako je graf numerisan, ako pustimo DFS iz čvora b, niz Idx će izgledati: (2, 1, 3, 4, 5, 6, 8, 7). To znači da su svi čvorovi posećeni, a redosled posete je b-a-c-d-e-f-h-g.
Ovako opisan algoritam radi samo za povezane grafove.
Obilasci nepovezanih grafova se rešavaju uz pomoć FullDFS Procedure.